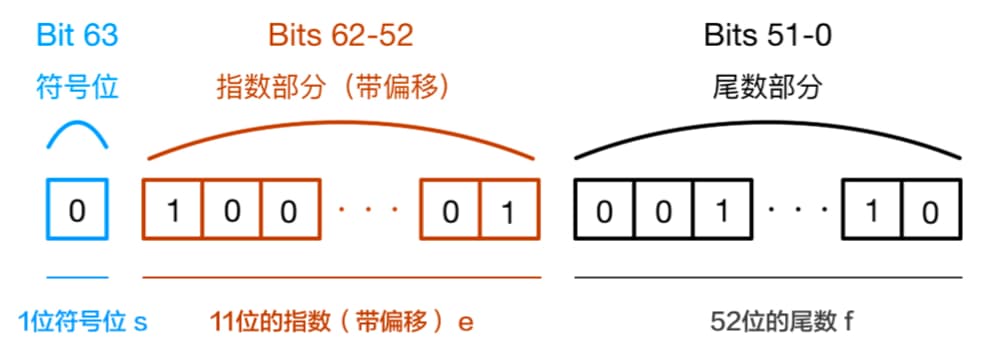
JavaScript里的数字采用的是 IEEE 754 标准的 64 位双精度浮点数,该标准对于64位的浮点数在内存中的表示如下:
- 第0位:符号位, s 表示 ,0表示正数,1表示负数;
- 第1位到第11位:储存指数部分, e 表示 ;
- 第12位到第63位:储存小数部分(即有效数字),f 表示;
因此JavaScript在处理运算的时候过程如下:
0.1 + 0.2 = 0.3首先将十进制的 0.1 和 0.2 转换为二进制:
0.1 -> 0.0001100110011001100110011001100110011001100110011001101
0.2 -> 0.001100110011001100110011001100110011001100110011001101IEEE 754 标准中,浮点数小数部分最多有效存储53个位,因此得到计算如下:
上述两者相加
0.0100110011001100110011001100110011001100110011001100将得到的数字再转换为十进制即为:
0.2999999999999971578290569595992565155029296875
// 四舍五入后即为:0.3因此,JavaScript在对一些要求计算精度高的需求里就会出现精度偏差问题,其实不只是JavaScript,只要使用了 IEEE 745 浮点数表示法的编程语言都会存在这个问题,只不过在这些语言里已经封装好了方法避免精度的问题,而JavaScript是一门弱类型的语言,从设计之初就没有考虑对浮点数有严格的限制,因此才会在如今前端广泛流行下暴露这个问题。
对应的解决办法也有,可以直接用Math.js库来解决精度计算的问题。
什么是 IEEE 754
全称为:IEEE二进制浮点数算术标准(ANSI/IEEE Std 754-1985),是20世纪80年代最为广泛使用的浮点数运算标准。
它规定了四种表示浮点数值的方式:
单精确度(32位);
双精确度(64位); – JavaScript采用的标准
延伸单精确度(43比特以上);
延伸双精确度(79比特以上);